منظور از تنش صفحه ای ، کرنش صفحه ای و تقارن محوری چیست ؟
به طور کلی در محیط پیرامون ما تمامی المان ها دارای سه بعد می باشند اما گاهی اوقات تحت شرایط خاصی این امکان وجود دارد که به منظور ساده سازی، المان های سه بعدی را به صورت دو بعدی در نظر بگیریم و در مدل سازی های خود در نرم افزار آباکوس به جای تعریف مسئله در سه بعد آن را در دو بعد به صورت تنش صفحه ای ، کرنش محوری یا تقارن محوری تعریف نماییم.
در این آموزش با پرتال جامع مهندسی عمران همراه باشید تا با مفاهیم تنش صفحه ای ، کرنش صفحه ای و تقارن محوری آشنا شوید.
توجه : برای دانلود ویدیو آموزش نرم افزار اباکوس با مدلسازی یک مثال کاربردی اینجا کلیک کنید.
منظور از تنش صفحه ای چیست ؟
در صورتی که در یک المان سه بعدی نسبت یک بعد به هر یک از دو بعد دیگر از 1/0 کوچکتر باشد و بارگذاری در راستای دو بعد بزرگتر اعمال شود، می توان مسئله را به صورت دو بعدی در نظر گرفت و فقط دو بعدی را در نظر گرفت که دارای ابعاد بزرگتری می باشند.
به عنوان مثال در شکل زیر شرایط تنش صفحه ای حاکم می باشد.
در این حالت مولفه های زیر از تنش و کرنش صفر می باشد و رابطه بین ماتریس تنش و ماتریس کرنش نیز به صورتی که در زیر آورده شده است می باشد.
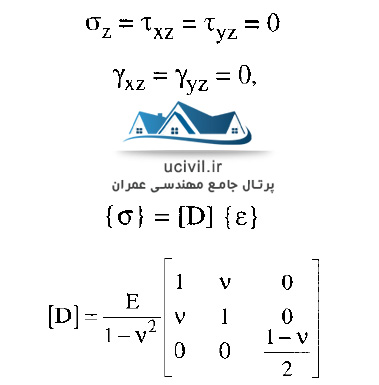
منظور از کرنش صفحه ای چیست ؟
به طور کلی در صورتی که یک بعد از المان سه بعدی نسبت به دو بعد دیگر خیلی بزرگتر باشد و بارگذاری در راستای بزرگترین بعد اعمال شود شرایط کرنش صفحه ای حاکم می باشد و در مدل سازی خود می توانیم دو بعد کوچکتر را در نظر بگیریم.
در این حالت کرنش در راستای بزرگترین بعد صفر می باشد.
اگر بزرگترین بعد در راستای z باشد مولفه های زیر از تنش و کرنش صفر می باشد و رابطه بین ماتریس تنش و ماتریس کرنش نیز به صورتی که در زیر آورده شده است می باشد.
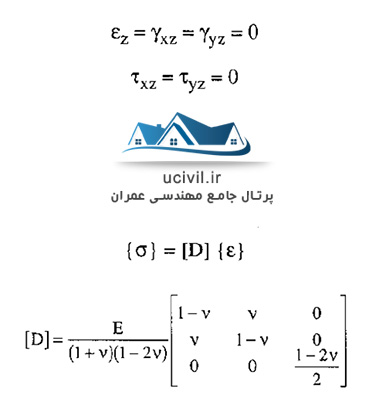
منظور از تقارن محوری چیست ؟
جسم متقارن به جسمی گفته می شود که از دوران یک سطح دو بعدی حول محور تقارن ایجاد شود.
در صورتی که دو شرط تقارن در هندسه و بارگذاری نسبت به یک محور تقارن به صورت هم زمان وجود داشته باشد می توان مسئله را از نوع تقارن محوری دانست.
به عنوان یک مثال ساده یک مخزن استوانه ای تحت تنش کششی را در نظر بگیرید.
در صورتی که شعاع قاعده مخزن استوانه ای برابر r و ارتفاع آن h باشد می توان این جسم سه بعدی را در نرم افزار آباکوس به صورت مدل دارای تقارن محوری در نظر گرفت که دارای دو بعد می باشد که عرض آن برابر 0.5r و ارتفاع آن برابر h می باشد که تحت تنش کششی قرار گرفته است.
