روش حل ضمنی (Implicit) در حل معادلات غیر خطی

در روش حل ضمنی برای رسیدن به همگرایی (Convergence) پاسخ، اعمال یک­ باره بار امکان پذیر نیست و بار باید به صورت مرحله ­ای و جزء به جزء به مدل اعمال شود. در این روش بارگذاری به صورت جزء بارگذاری به مدل اعمال می شود که تعادل در زمان t+∆t مطابق رابطه 1 می­ باشد.

پیشنهاد مطالعه : روش تحلیل صریح (Explicit) در اجزاء محدود

رابطه 1

که در آن R}_t+∆t} بردار نیروهای خارجی اعمالی به سیستم و F}_t+∆t} بردار نیروهای داخلی معادل با تنش در المان ها است.

از آنجا که نیروهای معادل داخلی به تاریخچه جابه­ جایی ­های گره ­ای بستگی دارند، حل معادله غیر خطی 1 نیاز به تکرار و خطا دارد تا تعادل کامل برقرار شود. برای این منظور به عنوان مثال نرم ­افزار آباکوس از روش نیوتن-رافسون (Newton Raphson mehod) استفاده می کند.

روش نیوتن-رافسون که معمولا به آن روش نیوتن (Newton’s method) اطلاق می شود روشی برای یافتن ریشه های معادلات جبری غیر خطی است. برای حل معادله غیر خطی f(x)=0، نقطه x₁ را روی منحنی شکل 1 در نظر می­ گیریم، شیب منحنی در نقطه x₁ برابر df(x₁)/dx است. بنابراین معادله مماس بر منحنی در مختصات ((x₁,f(x₁) مطابق رابطه 2 می ­باشد.

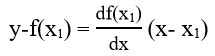
رابطه 2

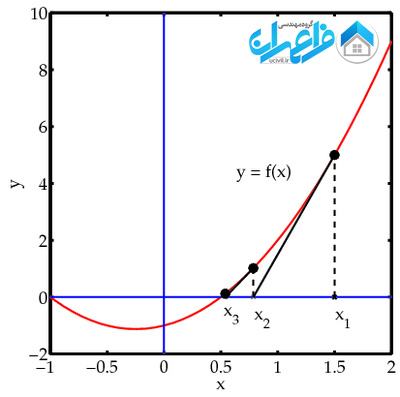
شکل 1

در y=0 خط مماس بر منحنی در نقطه x₁ محور x را در x₂ قطع می کند بنابراین معادله 2 به معادله 3 تبدیل می شود.

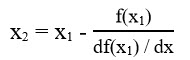
رابطه 3

در واقع ریشه تابع (f(x نقطه ­ای می باشد که در آن، منحنی محور x را قطع می ­کند. بنابراین برای دست یافتن به ریشه تابع در این روش، فرآیند ذکر شده باید تکرار شود تا به ریشه معادله همگرا شود. طرح کلی رابطه 3 با استفاده از روش تکرار نیوتن به صورت رابطه 4 می باشد.

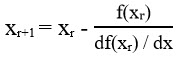
رابطه 4

فرآیند تکرار در روش نیوتن-رافسون زمانی متوقف می شود که رابطه 5 برقرار شود.

رابطه 5

که در آن ɛ مقدار خطا مد نظر می باشد که معمولا مقدار کمی است.

در نرم افزار آباکوس برای اینکه همگرایی حل با پیش فرض­ های نرم افزار انجام شود نیاز به تکرار و خطا با نموهای زمانی بسیار کوچکتر از ^5-10 ثانیه است. این مقدار نمو زمانی کوچک، هزینه و زمان حل را برای مدل های بزرگ نامعقول می کند. برای یک مسئله غیرخطی هر نمو زمانی نیاز به چندین تکرار دارد تا خطای محاسبات در محدوده مورد نظر قرار گیرد. برای این منظور نیاز است تا مجموعه ای از معادلات به صورت همزمان حل شوند و یک تصحیح C}_j} برای نمو جابجایی u}_j∆} ترتیب داده شود تا همگرایی حل صورت گیرد.

رابطه 6

که در آن k]_j] ماتریس سختی مماسی در ابتدای نمو زمانی، M]_j] ماتریس جرم مدل و پارامتر آخر در رابطه بالا نیز بردار شتاب می باشد.

تکرارها تا جایی که نیروهای باقی مانده و تصحیحات مربوط به جابجایی در محدوده تعریف شده قرار بگیرند، ادامه می یابد. با این وجود اگر مدل دارای ناپیوستگی های بزرگ، تماس و یا اصطکاک لغزشی باشد، به تعداد تکرار زیاد نیاز است. در همین راستا به علت ضعف این الگوریتم حل، روش صریح به عنوان ابزار مناسبی برای تحلیل سیستم های غیرخطی با تغییر شکل­ های بزرگ استفاده می ­شود. هر چند ممکن است مقدار نموهای زمانی در روش ضمنی با روش صریح برابر باشد، ولی به دلیل حل همزمان معادلات، هزینه محاسباتی در روش ضمنی بسیار بیشتر است و گاهی اوقات نیز همگرایی حل صورت نمی گیرد. هر تکرار در روش حل ضمنی نیاز به حل گسترده ­ای از معادلات خطی مربوط به مدل را دارد که به محاسبات قابل توجه و حافظه زیاد نیاز دارد، مخصوصا زمانی که اندازه مدل در نرم ­افزار بزرگ باشد، ملزومات حل معادلات به شدت افزایش می ­یابد که در عمل با توجه به توان کامپیوترهای رایج مصرفی و مقدار حافظه آنها، این کار امکان پذیر نمی ­باشد.

به طور خلاصه می توان گفت که در روش حل ضمنی ، مجموعه معادلات سیستم به روش مستقیم حل می‌شوند، به عبارت دیگر در روش حل ضمنی ، ماتریس سختی برای کل سازه تشکیل شده و برای هر گره جابجایی متناظر با آن به‌دست می‌آید و حل مسأله بر مبنای معکوس کردن ماتریس سختی استوار است.

پیشنهاد مطالعه : آشنایی با زمان حل در نرم افزار آباکوس