آشنایی با میرایی هیسترزیس و رایلی با نمودارهای مربوطه

در این نوشته تصمیم داریم به انواع میرايي در مصالح شامل دو نوع میرایی هیسترزیس و میرایی رایلی بپردازیم، با ما همراه باشید.

بخش عمده ای از انرژی گسترش يافته در يك محيط ژئوتكنیکی صرف غلبه بر اصطكاك بـين ذرات و بخشي دیگر سبب پيدايش كرنش های برگشت ناپذير (پلاستیک) می شود. لذا با انتشار موج در درون يك محيط ژئوتكنیکی به تدريج از انرژي آن كاسته شده و به عبارتي ميرا مي گردد. چرا كه در غیر اين صورت، اعمال یک نيرو بر یک سيستم، سبب نوسان آن تا مدت نامحدودی می گردد.

بدین ترتیب میرايی مصالح به عنوان جزء لاينفكي از ذات مصالح ژئوتكنيكي تلقي می گردد. عدم توجه به اين پارامتر در تحلیل های دیناميكي می تواند نتايج را تحت تأثیر قرار داده و پاسخ هاي غیر قابل قبولي را به دست دهد.

پیشنهاد مطالعه: تاثیر میراگر در مقاوم سازی لرزه ای ساختمان های فولادی

به طور كلی در يك تحليل دیناميكي میرايي را مي توان به دو دسته زیر تقسیم بندی نمود :

میرایی هیسترزیس

میرایی هیسترزیس در واقع ميرايي طبيعی مصالح ژئوتكنيكي بوده و به نوعي جزئي از خصوصـيات ذاتی آن محسـوب مي شود. از آنجا كه در تحليل های عددی از مدل هاي برگرفته از رفتار واقعي خاك با اعمال فرضيات ساده كننـده اسـتفاده مي شود، تنها برخي مدل هاي رفتاري غير خطي اين امكان را دارند كه در زمان تحليل ديناميكي اين نوع از ميرايي را به طور دقيق در مدل اعمال نمايند.

میرایی هیسترزیس خاك مستقل از فركانس است امـا در عـين حـال اسـتفاده از آن در تحليل دیناميكی داراي اشكالاتي نیز می باشد اول اينكه بسياری از توابع هيسترزيس ساده، زمانی كه در معرض چندين مـوج قـرار مي گيرند، تمامی مؤلفه ها را به طور يكسان ميرا نمي كنند. دوم اينكه توابع هيسترزيس اصولاً وابسته به مسير تـنش هسـتند كه باعث مي شود تفسير نتايج بسیار مشكل شود. با اين حال در حالت ايده آل در صورتي كه يك مدل رفتاری طوری عمل كند كه بتوان با تقريب خوبی آن را نمايندۀ واقعی رفتار هیسترزیس خاك دانست، دیگر نیازي به اعمال هیچ گونه ميرايي اضافي نخواهد بود.

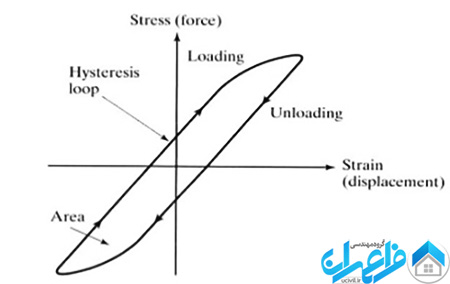
شکل 1 – حلقه هیسترزیس – Hysteresis Loop

میرایی هیسترزیس را مي توان از طريق تعريف يك سری توابع پيش فرض برای توليد منحنی كاهش مدول برشی در زمـان تحلیل دیناميكي نیز به مدل رفتاری افزود. در اين حالت لازم است براي تعیین پارامترهای اين توابع از داده های واقعی جهت تطبيق منحنی كاهش مدول برشی و افزايش میرايی استفاده نمود.

میرايی مكانيكی

در اغلب مواقع استفاده از مدل هاي رفتاري غیر خطي كه قادر باشند ميرايی هیسترزيس را در مـدل لحـاظ كننـد با صعوبت هاي زیادی همراه بوده و در برخی موارد نيز مدل، قابليت ارائه این نوع از میرايي را ندارد. در اين حالت از ميرايي مكانيكی براي بررسي رفتار ديناميكی سازه استفاده مي شود.

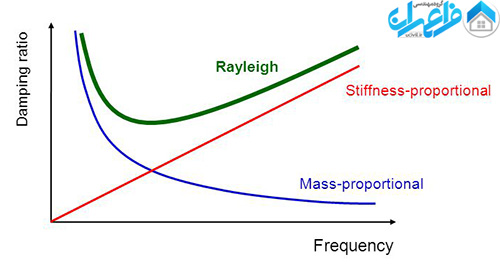
شکل 2 – میرایی رایلی

میرایی رایلی (Rayleigh Damping) مرسوم ترين نوع میرايي مكانيكی است كه در تحليل های دیناميكی به كار گرفته مي شود. به طور كلي در برنامه هايي كه در حوزه ی زمان عمل مي كنند، معمولاً جهت فراهم كردن ميرايي كه تقريباً مستقل از فركانس است، از ميرايي رايلی استفاده می شود. اگر چه بنا به تعريف، ميرايي رایلي خود وابسـته بـه فركـانس اسـت ولي می توان پارامترهاي آن را در محدوده ای استفاده كرد كه اثرات وابستگي به فركانس تا حد ممكن كاهش يابد.

میرایی رایلی معمولاً برای میرا كردن مدهای نوساني طبيعی سیستم در تحليل سازه ها و محیط های پیوسته الاستيك به كار برده مي شود. بنابراين معادلات به فرم ماتریسي و به صورت رابطه زير بیان مي شوند :

رابطه 1

در اين رابطه C ماتريس میرايي و M ماتريس جـرم و K مـاتريس سـختی اسـت. α و β نيـز ضـرائب ثابـت ميرايی متناسب با جرم و سختي هستند.

برای يك سیستم با چند درجه ی آزادی در هر مود نوسانی با سرعت زاویه اي ω_i ، نسبت میرايي ξ_i را مي توان به صورت زیر محاسبه نمود :

رابطه 2

در شكل 3 تغييرات نسبت ميرايي (ξ_i) به ميرايي بحراني (ξ_min) در برابر سرعت زاويه ای (ω) نشان داده شده است. در اين شكل سه منحنی ارائه شده است. دو منحني نشان دهنده اثرات مؤلفه هاي سختي و جرم میرايي به تنهايی بوده و منحني سوم اثرات توأم اين دو مؤلفه را نشان مي دهد. همانطور كه در اين شكل مشـاهده مـي شـود در محـدوده ی فركانس دوراني كم، ميرايي متناسب با جرم غالب است در حالي كه در فركانس دوراني زیاد، ميرايي متناسب بـا سختي غالب خواهد بود.

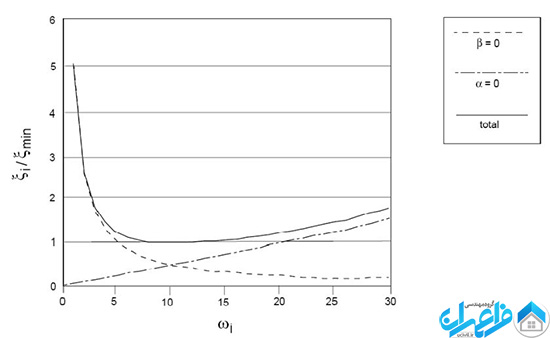
شكل 3 – تغييرات نسبت ميرايي بحراني اصلاح شده با سرعت زاویه اي

با توجه به آنكه ميرايي ذاتي مستقل از فركانس است مي توان دامنه فركانس هاي ارائه شده را طوري تعريف كـرد كـه میرايي عملاٌ ثابت بماند. براي این كار مي توان از بازه پایيني منحني میرايي رايلي كه در آن مقدار میرايي نسبتاٌ ثابت است استفاده كرد. این محدوده با مختصات زير توام خواهد بود :

رابطه 3 و 4

بنابراين در صورت معلوم بودن ميرايي و فركانس مورد نظر مي توان پارامترهاي میرايي رايلي را به صورت زیر محاسـبه نمود :

رابطه 5 و 6

در نهايت فركانسی كه در آن ميرايي تقريباً ثابت است به صورت زير تعيين می شود كه :

رابطه 7

باید توجه داشت كه در فركانسي معادل فركانس كمينه (f_min)، میرايي متناسب با جرم و ميرايي متناسب با سـختی، تقريبا هر كدام نيمي از ميرايي كل را فراهم مي كنند.

بنابراين به طور خلاصه جهت محاسبه ضرايب میرایی رایلی در ابتدا لازم است نسبت میرايي بحراني مصالح (ξ_min) بـا استفاده از نتايج آزمایش هاي آزمايشگاهي نظير سه محوری تناوبي تعیین گردد. براي این منظور مي توان از منحني هاي افزایش ميرايي نسبت به كرنش برشي استفاده كرد. مقدار فركانس (f_min) نيـز تركيبـي اسـت از فركـانس مـوج ورودي و مدهاي طبيعي سیستم كه با قضاوت مهندسي مابين فركـانس غالـب زلزلـه و فركانس هاي طبيعي اصـلي سـد انتخـاب می گردد.