روش های تعادل حدی تحلیل پایداری شیب های خاکی
در این پست ابتدا روش های تعادل حدی تحلیل پایداری شیب های خاکی را به اختصار توضیح می دهیم سپس به مقایسه روش های ذکر شده می پردازیم.
روش هاي تك قطعه ای
روش های تک قطعه ای به منظور تحلیل پایداری شیروانی های خاکی شامل روش های زیر می باشد :
- روش شیب های نامحدود
- روش دایره سوئدی
- روش سطح لغزش صفحه ای
در ادامه هر یک از سه روش ذکر شده را به اختصار شرح می دهیم :
روش شيب های نامحدود از روش های تعادل حدی
اين روش براي تحليل شيرواني هايي با طول نامحدود كاربرد دارد.
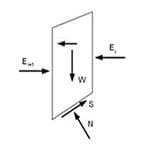
در اين روش صفحه گسيختگي يا لغزش به موازات شيب درنظر گرفته شده و مقادير نيروها در تمام صفحات عمود بر شيب (نظير صفحات A’-A و B’-B در شکل 1) مقادير يكساني خواهند داشت.
بدين ترتيب معادلات تعادل نيروهاي افقي و قائم، تنها براي يك طول واحد از اين شيب نوشته مي شود.
اصلي ترين اشكال اين روش آن است كه در آن از اثر وضعيت هندسي شيب در بالا و پايين آن صرف نظر و خاك، همگن در نظر گرفته شده است.
با اين حال اين روش براي شيب هايي كه از ارتفاع و طول زيادي برخوردارند و خاك نيز در محدوده سطح لغزش لايه بندي مشخصي ندارد، جواب هاي نسبتاً دقيقي به دست مي دهد.
شکل 1- نيروهاي وارد بر يك شيب نامحدود
روش دايره سوئدی (Φ = 0) از روش های تعادل حدی
اين روش يكي از قديمي ترين روش هاي برآورد ضريب اطمينان پايداري شيب ها است.
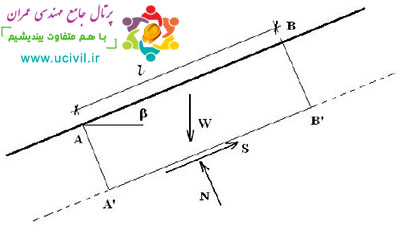
در اين روش سطوح لغزش به صورت دايره اي شكل و مصالح مورد بررسي فاقد زاويه اصطكاك داخلي فرض مي شوند (شکل 2)
بدين ترتيب با نوشتن يك معادله تعادل لنگر حول مركز دايره، ضريب اطمينان توده خاك در مقابل لغزش به دست مي آيد.
پس از ارائه روش سوئدي روش ديگري نيز با نام روش سوئدي اصلاح شده ابداع شده است كه مبناي آن روش قطعات مي باشد.
شکل 2- نيروهاي وارد بر يك سطح لغزش دايره اي در روش سوئدي
روش سطح لغزش صفحه ای از روش های تعادل حدی
اين روش عموماً در مورد شيرواني هايي به كار مي رود كه در آن وجود يك لايه خاك با ضخامت كم و با خصوصيات مقاومتي ضعيف نسبت به ساير لايه ها باعث بروز لغزش در شيب ميشود.
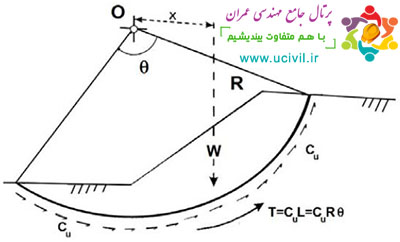
سطح لغزش در اين روش به صورت صفحه اي در نظر گرفته شده و ضريب اطمينان با استفاده از حل معادلات تعادل ، براي نيروهاي وارد بر آن محاسبه مي شود.
شكل 3 نمايي از فرضيات اين روش را نشان مي دهد.
شکل 3- نيروهاي وارد بر يك سطح لغزش صفحه اي
روش قطعات
روش های قطعات برای تحلیل شیب های خاکی شامل روش های زیر است :
- روش گوه ای
- روش اوليه قطعات يا روش فلينيوس
- روش سوئدی اصلاح شده
- روش ساده شده بیشاپ
- روش عمومي جانبو
- روش اسپنسر
- روش مرگنسترن و پرايس
در ادامه هر یک از 7 روش ذکر شده را به اختصار توضیح می دهیم :
روش گوه ای از روش های تعادل حدی
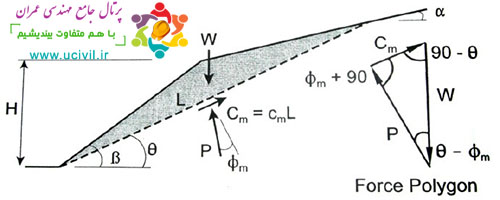
در اين روش هندسه سطوح لغزش فرضي به صورت يك مسير چند خطي در نظر گرفته مي شود.
بدين ترتيب نيروهاي وارده بر هر بلوك از اين توده لغزش، نظير آنچه در شكل 4 ديده مي شود، ترسيم و با نوشتن معادلات تعادل براي هر بلوك ضريب اطمينان پايداري شيب محاسبه مي گردد.
در حالتي كه گوه به صورت دو خطي در نظر گرفته مي شود معمولاً ناحيه مقاوم پايين دست وجود ندارد.
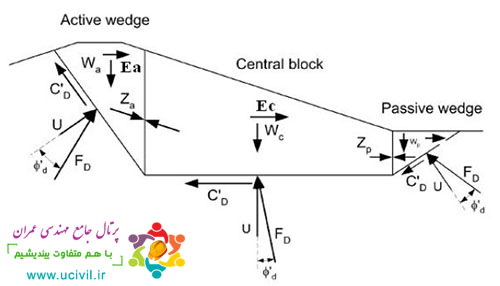
شکل 4- نيروهاي وارد بر بلوك هاي مختلف توده گسيخته شده در روش گوه اي
روش اوليه قطعات يا روش فلينيوس از روش های تعادل حدی Ordinary Method of Slice or Fellenius Method
روش اوليه قطعات يا روش فلينيوس به عنوان يكي از ابتدايي ترين روش هاي تحليل پايداري شيب با استفاده از روش قطعات محسوب مي گردد.
در اين روش با انتخاب سطح لغزش دايره اي و تقسيم توده لغزشي به قطعات قائم و با صرف نظر از نيروهاي بين قطعه اي، معادلات تعادل تنها براي لنگر نوشته شده و ضريب اطمينان پايداري بر همين اساس به دست مي آيد (شکل 5)
روش فلينيوس كه از اولين روش هاي ارائه شده براي تحليل پايداري شيب ها است، دقت بسيار پاييني در محاسبه ضريب اطمينان داشته و نه تنها براي تحليل هاي شبه استاتيكي بلكه براي تحليل پايداري استاتيكي سدهاي خاكي نيز توصيه نمي گردد.
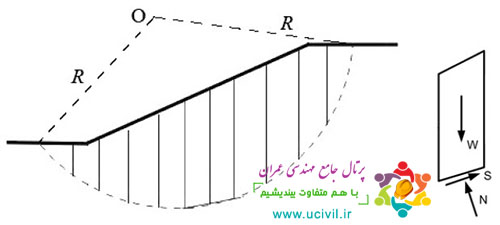
شکل 5- توده لغزشي و نيروهاي وارد بر يك قطعه نمونه در روش اوليه قطعات
روش سوئدی اصلاح شده از روش های تعادل حدی Modified Swedish Method
در اين روش ضريب اطمينان پايداري شيب صرفاً بر مبناي تعادل نيروها در دو جهت افقي و قائم محاسبه شده و جهت نيروهاي بين قطعه اي معمولاً به موازات شيب متوسط سطح خاكريز درنظر گرفته مي شود.
اين روش براي سطوح لغزشي غير دايره اي نيز كاربرد دارد.
روش ساده شده بیشاپ از روش های تعادل حدی Simplified Bishop Procedure
در روش بيشاپ ساده شده محاسبه ضريب اطمينان صرفاً براي سطوح لغزش دايره اي و با نوشتن معادلات تعادل نيرو در جهت قائم براي هر قطعه و همچنين تعادل لنگر حول مركز دايره براي مجموعه قطعات صورت ميپذيرد.
در اين روش از نيروي برشي بين قطعات صرف نظر شده و بنابراين نيروي بين قطعات فقط به صورت عمود بر سطح بين قطعات (به صورت افقي) در نظر گرفته مي شود.
بدين ترتيب نيروي زلزله كه معمولاً به صورت مولفة افقي شبه استاتيكي منظور مي شود در معادلات تعادل نيرو وارد نشده و صرفاً در معادلات تعادل لنگر، ايفاي نقش مي نمايند.
بنابراين نتايج اين روش براي تحليل شبه استاتيكي بيش از نتايج تحليل استاتيكي با خطا مواجه مي باشد.
علاوه بر اين، روش بيشاپ ساده شده سطوح گسيختگي را صرفا به صورت دايره اي در نظر گرفته و توانايي تحليل ساير اشكال را ندارد.
روش بيشاپ ساده شده براي خاك هاي چسبنده، اصطكاكي و چسبنده اصطكاكي به كار مي آيد.
نتايج مطالعات برخي محققين نشان ميدهد كه اين روش در تحليل استاتيكي از دقت قابل قبولي برخوردار است.
همچنين Wright و همکاران سال 1973 نشان داده اند كه ضريب اطمينان حاصل از روش بيشاپ ساده شده فقط در حدود 5 درصد با نتايج تحليل انجام شده به روش اجزاء محدود اختلاف دارد.
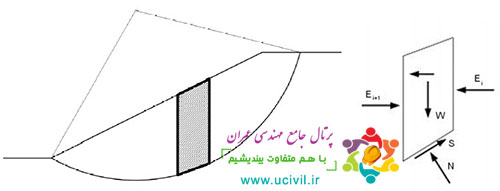
شکل 6- توده لغزشي و نيروهاي وارد بر يك قطعه نمونه در روش بيشاپ ساده شده
روش عمومي جانبو از روش های تعادل حدی Janbu’s Generalized method
در اين روش ضريب اطمينان پايداري شيب صرفاً بر مبناي تعادل نيروها در دو جهت افقي و قائم محاسبه شده و معادله لنگر تنها در محاسبه رابطه نيروهاي قائم و افقي بين قطعات به كار گرفته مي شود.
اين روش براي سطوح لغزش غير دايره اي نيز قابل استفاده مي باشد.
روش اسپنسر از روش های تعادل حدی Spencer’s method
در روش اسپنسر همه نيروهاي بين قطعات، تحت يك زاويه مشخص با محور افقي ، با يكديگر موازي فرض مي شوند.
مقدار اين زاويه و محل اثر نيروي برآيند بين قطعات به عنوان دو مجهول از حل دستگاه معادلات تعادل به دست مي آيد.
همچنين در اين روش نيروهاي عمود بر كف هر قطعه در جهت عمود بر سطح و در وسط قطعه درنظر گرفته مي شود.
در صورتي كه تعداد قطعات به اندازه كافي زياد باشد اين فرض تغيير چنداني در نتيجه نهايي ايجاد نمي كند.
از سوي ديگر در روش اسپنسر امكان در نظر گيري مولفة شبه استاتيكي نيروي زلزله و همچنين سطوح لغزشي غير دايره اي وجود دارد.
بدين ترتيب در اين روش، تعادل نيروها در جهت افقي و قائم و همچنين تعادل لنگرها حول هر نقطه دلخواه ارضاء مي گردد.
روش اسپنسر يك راه حل كامل براي تحليل پايداري شيب ها به روش تعادل حدي است و در بسياري از دستورالعمل هاي طراحي مورد توجه واقع شده است.
با اين حال از آنجايي كه براي حل آن بايد از شيوه سعي و خطا براي دستيابي به جواب نهايي استفاده گردد، الزاماً مي بايست نرم افزارهاي كامپيوتري به كار گرفته شود و حل دستي آن بسيار دشوار و تقريبا غير ممكن است.
روش مرگنسترن و پرايس از روش های تعادل حدی Morgenstern & Price method
كليات روش مرگنسترن و پرايس مشابه روش اسپنسر مي باشد.
با اين تفاوت كه در اين روش زاويه نيروي برآيند بين قطعات نسبت به افق، به صورت ضريبي از يك تابع فرضي درنظر گرفته شده كه اين ضريب به عنوان يك مجهول در معادلات تعادل وارد مي شود.
اين روش بعدها با تغييرات اندكي توسط چن و مرگنسترن اصلاح گرديد.
انتخاب روش مناسب تحليل
انتخاب روش مناسب براي تحليل پايداري يك شيرواني خاكي اصولاً تابع اهداف مورد نظر و نيز ابزارهاي در دسترس مي باشد.
برخي از اين روش ها براي تحليل هاي دستي و اوليه و كنترل صحت تحليل هاي كامپيوتري مناسب هستند.
برخي ديگر براي تحليل مكانيزم گوه اي برتري داشته و گروهي از اين تحليل ها با توجه به پيچيدگي ها و تحليل هاي متعدد و زمانبري كه نياز دارند تنها در قالب نرم افزارهاي كامپيوتري كاربرد دارند.
آنچه كه در انتخاب روش مناسب براي تحليل شبه استاتيك حائز اهميت است آنست كه روش منتخب بايد به خوبي نيروي بين قطعات را مورد توجه قرار داده باشد.
بديهي است روش هايي كه از نيروهاي بين قطعات صرف نظر مي كنند شرايط مناسبي براي تحليل شبه استاتيكي ندارند.
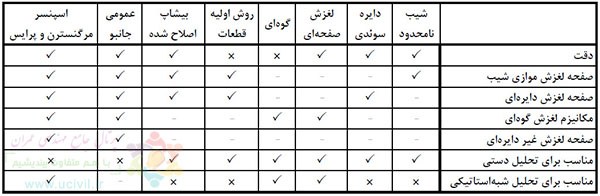
جدول 1 مباني و فرضيات و جدول 2 قابليت و محدوديت هاي هريك از روش هاي فوق را به اختصار نشان مي دهد.
همانطور كه در اين جداول مشخص است در ميان روش هايي كه كليه معادلات تعادل نيروها و لنگر را ارضاء مي كنند، دو روش مرگنسترن – پرايس و اسپنسر توجه مناسبي به نيروي بين قطعات، محل اثر آنها و زاويه برايند آنها با افق داشته اند و براي تحليل هاي شبه استاتيك مناسب تر هستند.
در تحليل هاي پايداري لازم است شكل سطوح لغزش محتمل به طور ويژه مورد توجه قرار گيرد.
بدين معنا كه در مدلسازي عددي علاوه بر سطوح لغزشي كه در نرم افزارها (عمدتاً به صورت دايره اي) در نظر گرفته مي شود، ساير اشكال سطوح گسيختگي محتمل از جمله گوه اي، صفحه اي يا نامشخص نيز در محاسبه ضريب اطمينان پايداري لحاظ گردد .
اين مسأله به ويژه در مواردي كه لايه هاي ضعيف يا با قابليت روانگرايي در پي (يا احتمالاً بدنه سد) وجود داشته باشد، حائز اهميت خواهد بود.
در حل اينگونه مسائل، چنانكه جدول 2 نشان مي دهد روش هاي مرگنسترن -پرايس و اسپنسر به دليل عدم محدوديت در شكل سطوح لغزش، نسبت به ساير روش هاي موجود برتري دارند.
جدول 1- مقايسه فرضيات روش هاي مختلف تعادل حدي براي محاسبه ضريب اطمينان با استفاده از معادلات تعادل
جدول 2- مقايسه ويژگي هاي روشهاي مختلف تعادل حدي
